极限教案

导读：　极限教案(共5篇)极限与连续教案第一章 极限与连续一、极限（一）、 数列的极限1、数列：无穷多个数按一定顺序排列成：x1,x2,x3xn称为数列，记为{xn}其中xn称为数列的一般项或通项。 11111,,, 通项xn＝n 有极限0 248162345n1②、2,,, 通项xn＝ 有极限1 23...

欢迎来到中国招生考试网http://www.chinazhaokao.com/成考报名栏目，本文为大家带来《极限教案》，希望能帮助到你。

极限教案(一)
极限与连续教案

第一章 极限与连续

一、极限

（一）、 数列的极限

1、数列：无穷多个数按一定顺序排列成：x1,x2,x3xn称为数列，记为{xn}其中xn称为数列的一般项或通项。 11111,,, 通项xn＝n 有极限0 248162

345n1②、2,,, 通项xn＝ 有极限1 234n例如：①、

3、5、7、 通项xn＝2n1 无极限 ③、1、

4、6、8、 通项xn＝2n 无极限 ④、2、

当n无限增大时，xn聚集于一点（无限地接近一个常数），我们称这个常数为该数列的极限（或称该数列收敛）（如①②），否则称该数列发散（如③④）

2、数列极限的定义

设有数列xn和常数A，如果对任意给定的ε > 0, 总存在正整数N , 使得当n >N时, 不等式|xnA| 恒成立，则称常数A为数列xn的极限（或称数列xn收敛于A），记作limxnA n

定义简化： 0, N0 , 使得当n >N时, 有|xnA| 恒成立，则称A为数列xn的极限，limxnA n

345,, 的极限为1 234

n11111| ，取N＝[] ，则当n > N＝[] 时,有 证：0,要使|nn

n1n1|1| ，即lim1 nnn

当0.1时，只要n10

当0.01时，只要n100

当0.00001时，只要n100000 例1、用定义证明2,

3、数列极限的几何意义

（二）、数列极限的性质

1、唯一性：如果一个数列有极限，则此极限是唯一

2、有界性：收敛数列一定有界，反之不成立；即有界数列不一定收敛。

例如： 1、0、1、0、……虽有界，但发散

3、数列极限的四则运算

ynb 则 设有limxna limnn

⑴、lim(xnyn)limxnlimynab nnn

⑵、lim(xn.yn)limxn.limynab nnn

xnaxnlimn⑶、lim(b0) nylimybnnn

4、数列极限存在的准则：

准则Ⅰ（夹逼定理）

如果数列xn，yn，zn满足不等式xnynzn(n1,2,3...)且

limxnlimzna，则limyna nnn

准则Ⅱ：单调有界数列必有极限。

5123n25n1n3001 例2、求极限lim2limn6n4n7n47600262nn

（三）、 函数的极限

1、当x 时函数f(x)极限的定义：

0, M0 , 使得当|x|M时, 不等式|f(x)A| 恒成立，则称A为函数f(x)当x的极限，记为limf(x)A 3x

2、当xx0 时函数f(x)极限的定义：

0, 0 , 使得当0|xx0|时, 不等式|f(x)A| 恒成立，则称A为函数f(x)当xx0的极限，记为limf(x)A

xx0

3、函数的极限limf(x)存在且等于A的充分必要条件是：左极限limf(x)与右极限xx0xx0

xx0limf(x)都存在且等于A。 

即有limf(x)limf(x)A limf(x)A xx0xx0xx0

即：函数的极限存在的充分必要条件是

f(x00)f(x00) 左右极限相等

4、函数极限的几何意义

1,x0 x,x0

f(x)lim11 解：lim例3、f(x)x0x0

x0limf(x)limx0 x0

x0f(x)不存在  左右极限存在，但不相等 lim

x23x4x1x1例4、f(x)3x11x2

3x3x2x1

(x1)(x4)x23x4lim(x4)5 lim解：f(10)limx1x1x1x1x1

(3x1)2 f(10)limx1

f(10)f(10) 故limf(x)不存在 x1

(3x1)5 而f(20)limx2

(f(20)limx23x3)5 x1

x2f(20)f(20) 故limf(x)5

（四）函数极限的性质【极限教案】

1、唯一性定理：如果limf(x)存在，则此极限值必唯一 xx0(x)

2、夹逼定理：设函数f(x)，g(x)，h(x)在x0某一邻域内有定义，如果g(x)f(x)h(x) 且limg(x)limh(x)A，则limf(x)存在，且limf(x)A xx0(x)xx0(x)xx0(x)xx0(x)

3、函数极限的四则运算

g(x)B 则 设有limf(x)A lim

⑴、lim[f(x)g(x)]limf(x)limg(x)AB

⑵、lim[f(x)g(x)]limf(x)limg(x)AB f(x)limf(x)A⑶、lim g(x)limg(x)B

⑷、lim[Cf(x)Climf(x) 其中C为常数

⑸、lim[f(x)][limf(x)] 其中n为常数 nn

（五）、两个重要极限

sinxtanx1cosx11 或lim1 或lim x0x0x0xx2x2

11x2、lim(1)e 或lim(1x)xe xx0x

tanxsinx1sinx1lim.lim.lim1 例5、limx0x0xxcosxx0xx0cosx

1xxx*2sin2sin2sin2

1cosx1lim()21*11 lim例6、limlimx0x0x0xx22x0x22x2()2

22

x2x2222例7、lim(1)lim[(1)]e xxxx

（六）、无穷大量与无穷小量 1、lim

1、 无穷大量定义：

limf(x) 表示变化的趋势为 xx0(x)

2、无穷小量

xx0(x)limf(x)0 表示变化的趋势为0

3、无穷小量与无穷大量的关系：

10 f(x)

1 ②、若limf(x)0 则limf(x)①、若limf(x) 则lim

4、无穷小量的性质：

①、有限个无穷小量的和或差仍为无穷小量。

②、有限个无穷小量的积仍为无穷小量。

③、任一常数与无穷小量之积是无穷小量。

④、无穷小量与有界变量之积是无穷小量。

5、无穷小量的比较：

limf(x)0 limg(x)0

0则称f(x)是比g(x)较高阶的无穷小f(x)则称f(x)是比g(x)较低阶的无穷小lim g(x)c0则称f(x)是比g(x)同阶的无穷小1则称f(x)是比g(x)等阶的无穷小【极限教案】

熟记下列等价无穷小(x0)

1、sinxx

sinaxax 2、tanxx

3、ex1x x 4、ln(1x)

11x1 6、xx1 2n

arcsinxx12x 8、7、1cosx arctanxx25、x

例8、比较两个无穷小量

①、当x0时，sin(xx2)与x比较

sin(xx2)xx2

lim(1x)1 （等价无穷小） limlimx0x0x0xx

2②、当x0时，x与sinx比较

x2x2

limx0 limlimx0x0sinxx0x

x2比sinx较高阶的无穷小

例9、当x0时，x1与下述函数进行比较，哪些是高阶无穷小？哪些是低价无穷小？哪些是同阶无穷小？哪些是等阶无穷小？

①x ②x1x22 ③x ④ ⑸xsin ⑹x 2xx1

解：①limx01x111x1lim 同阶 limx0xx(x1)x0x12

2(1x1)x12lim1 等阶 limx0x0x0xx1x(x1)21x1x1③、limlim 低价 x0x02x2x(x1)②、lim

x2 比x1高阶的无穷小

④、limx01x1x11 等阶 limx0xx

x1

⑸、limx0x1limlim 低价 x0211x012xsinxsinxsinxxx1x111xx1limlim0 高阶 ⑹、limx0x0xxx01

x

几种求极限的方法：

极限教案(二)
高中数学《函数的极限》教案

课 题：2.3函数的极限(二)

教学目的：

1.理解函数在一点处的极限，并会求函数在一点处的极限． 2.已知函数的左、右极限，会求函数在一点处的左右极限． 3.教学重点：掌握当xx0时函数的极限

教学难点：对“xx0时，当xx0时函数的极限的概念”的理解 授课类型：新授课课时安排：1课时 教 具：多媒体、实物投影仪 内容分析：

上节课我们学习了当x趋向于∞即x→∞时函数f(x)的极限.当x趋向于∞时，函数f(x)的值就无限趋近于某个常数a.我们可以把∞看成数轴上的一个特殊的点.那么如果对于数轴上的一般的点x0，当x趋向于x0时，函数f(x)的值是否会趋近于某个常数a呢？ 教学过程：

一、复习引入： 1.数列极限的定义：

一般地，如果当项数n无限增大时，无穷数列{an}的项an无限趋近于某个．．．．．常数a（即ana无限趋近于0），那么就说数列{an}以a为极限，或者说a是数列{an}的极限．记作limana，读作“当n趋向于无穷大时，an的极限等

n

于an∞”表示“n趋向于无穷大”，即nana有



时也记作：当n∞时，ana． 2.几个重要极限： （1）lim

1

0 （2）limCC（C是常数）

nnn

n

n

（3）无穷等比数列{q}（q1）的极限是0，即 limq0(q1)n

3.函数极限的定义:

(1)当自变量x取正值并且无限增大时，如果函数f(x)无限趋近于一个常

数a，就说当x趋向于正无穷大时，函数f(x)的极限是a. 记作：

x

limf(x)=a，或者当x→+∞时，f(x)→a.

(2)当自变量x取负值并且绝对值无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于负无穷大时，函数f(x)的极限是a. 记作

x

limf(x)=a或者当x→－∞时，f(x)→a.

(3)如果

x

limf(x)=a且limf(x)=a，那么就说当x趋向于无穷大时，函

x

数f(x)的极限是a，

记作：limf(x)=a或者当x→∞时，f(x)→a.

x

4.常数函数f(x)=c.(x∈R)，有limf(x)=c.

x

limf(x)存在，表示limf(x)和limf(x)都存在，且两者相等.所以limf(x)

x

x

x

x

中的∞既有+∞，又有－∞的意义，而数列极限liman中的∞仅有+∞的意义x

二、讲解新课： 1.研究实例

(1)探讨函数yx，当x无限趋近于2时的变化趋势． 当x从左侧趋近于2时，记为：x2．



2



当x从右侧趋近于2时, 记为：x2.

2

2

2

x2,（右极限）limx2,因此有limx2． 发现（左极限）lim

x2

x2

x2

(2)我们再继续看

x21y,当x无限趋近于1（x1）时的变化趋势:

x1

x21yx1,(x1),当x从左侧趋近于1时，即x1时，y2．

x1

当x从右侧趋近于1时, 即x1时，y2．



x21

即（左极限）limlim(x1)2，

x1x1x1x21

（右极限）limlim(x1)2

x1x1x1

x21

limlim(x1)2

x1x1x1

x1(x0)



(3)分段函数f(x)0(x0)当x→0的变化趋势.

x1(x0)

f(x)1 ①x从0的左边无限趋近于0，则f(x)的值无限趋近于－1.即lim

x0

f(x)1 ②x从0的右边无限趋近于0，则f(x)的值无限趋近于1. 即lim

x0

可以看出

xx0

limf(x)limf(x)，并且都不等于f(0)0．象这种情况，

xx0

就称当x0时，f(x)的极限不存在．

2. 趋向于定值的函数极限概念：当自变量x无限趋近于x0（xx0）时，如果函数yf(x)无限趋近于一个常数a，就说当x趋向x0时，函数yf(x)的极限是a，记作limf(x)axx0

特别地，limCC；limxx0xx0xx0

3. limf(x)alimf(x)limf(x)a

xx0

xx0

xx0

f(x)a表示当x从左侧趋近于x0时的左极限，limf(x)a表其中lim

xx0

xx0

示当x从右侧趋近于x0时的右极限三、讲解范例：

例1求下列函数在X＝0处的极限

2x,x0

xx21

（1）lim2 （2）lim （3）f(x) 0,x0x02xx1x0x

1x2,x0

x21x1

lim1 解：（1）lim2

x02xx1x02x1

（2）lim

x0

xxx

1,lim1lim不存在． x0x0xxx

2x,x0

（3）f(x) 0,x0

1x2,x0

2x

limf(x)lim(1x)1,limf(x)lim21 

x0

x0

x0

x0

limf(x)limf(x)1limf(x)1．



x0

x0

x0

四、课堂练习：

1．对于函数y2x1填写下表，并画出函数的图象，观察当x无限趋近于1时的变化趋势，说出当x1时函数y2x1的极限

2．对于函数yx21填写下表，并画出函数的图象，观察当x无限趋近于3时的变化趋势，说出当x3时函数yx21的极限

3.求如下极限：

x21(x1)3(13x)2

lim2(sinxcosxx) ⑴lim2; ⑵lim; ⑶23x12xx1x0x2xx

2

⑷lim

x4

2x3x2

1a2xa

;⑸lim（a0）; ⑹lim x0xx0x

x21x12(x1)3(13x)x3

lim ⑵ limlim3 答案：⑴lim2

x12xx1x12x1x0x012x3x22x3

24

⑶lim2(sinxcosxx)2

⑷

x4x2x32

2

11⑸ ⑹lim不存在．

x0xx0x2a

五、小结 ：

七、板书设计

极限教案(三)
极限与连续教案

安徽中医药高等专科学校教案

第一章 极限与连续

1．1极限的概念

1.1.1函数的概念

1. 函数的定义

圆的面积A与半径r之间的关系A=r表示。这里A与r都是变量，当半径r变化时。圆的面积A作相应的变化

定义1.1 设x与y是两个变量，D是非空实数集，如果对于任意xD,按照某个对应法则f,变量y有惟一确定的实数与之对应，记作y=f (x) 则称f是定义在D上的函数（映射）,x称为自变量，y称为因变量，D称为函数f的定义域.数集M=f(D)={f(x)｜xD}称为函数f的值域。

2．函数的定义域

1）在分式中，分母不能为零

2）在根式中，负数不能开偶次方根

3）在对数中，真数必须大于零

4）三角函数和反三角函数

三角函数 ：正切xk1 

余切xk

反三角函数：正（余）弦1x1

正（余）切x(,) 2

x的定义域 x2

xx解：要使f(x)lg有意义，必须使>0即x>0或x<0 x2x2

3.函数几种特性

1)有界性 例 求函数f(x)lg

若存在正数M,使得在区间I上f(x)M,则称f(x)在I上有界.

例如f(x)sinx在(,)上有界,因为sinx1而(x)1在(0,1)内无界. x

2)单调性

设函数f(x)的定义域为D,区间ID如果对于区间I任意两点x1及x2.

当x1<x2时恒f(x1)<f(x2) 则称函数f(x)在区间I上是单调增的.

当x1<x2时恒f(x1)>f(x2) 则称函数f(x)在区间I上是单调减的.

利用导数的判别 1如果在(a,b)内f(x)0则f(x) 2如果在(a,b)内f(x)0则f(x)

3)奇偶性

设函数f(x)的定义域D关于原点对称(即xD,则必有xD)

对于f(x)f(x)恒成立,则称f(x)为偶函数

对于f(x)f(x)恒成立,则称f(x)为奇函数

例：

gln(x 的奇偶性)

f(x)ln(x

f(x)ln(x 1)

则f(x)f(x)ln(x(xln10

则f(x)f(x)

注: 1奇函数的代数和仍为奇函数，偶函数代数和仍为偶函数 2偶数个奇（偶）函数为偶函数，奇则奇 3一奇一偶为奇函数（乘积）

4）周期性

若存在不为零的数T，使得对于任意xTI，且f（x+T）=f（x），则称f（x）为周期函数。 4、分段函数

已知函数定义域被分成有限个区间，若在各个区间上表示对应规则的数学表达式一样，但单独定义各个区间公共端点处的函数值；或者在各个区间上表示对应规则的数学表达式不完全一样，则称这样的函数为分段函数。

其中定义域所分成的有限个区间称为分段区间，分段区间的公共端点称为分界点。

5、复合函数

在很多实际问题中，两个变量的联系有时不是直接的。例如，质量为m的物体，以速

12mv，即动能E是速度v的函数；而VV0gt，即速度v又2

12是时间t的函数，于是得Em(v0gt) 2度v0向上抛，其动能E

又如函数ysin2x，如果用M表示2x，那么函数y=sin2x可表示成y=sinM，而M=2x，这也说明了y与x的函数关系是通过变量M来确定的。

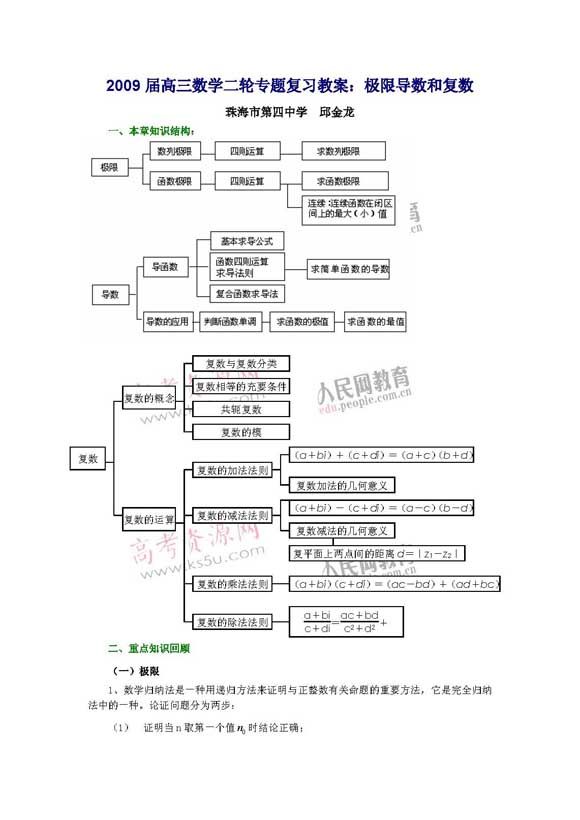
定义4 如果y是M的函数y=f（u），而u又是x的函数u(x)，通过u将y表示成x的函数，即yf[(x)]，那么y就叫做x的复合函数，其中M叫中间变量。

注意：函数ug(x)的值域应该取在yf(u)的定义域内，否则函数将失去意义。

1,) 例：y=lgu u=x+1 u(0,) x(内初等函数：由常数和基本初等函数经

过有限次四则运算或有限次复合步骤所构成的函数叫做初等函数。

例如：y y

二、基本初等函数（见课本p5）

定义 由五类基本初等函数和常数经过有限次四则运算或有限次复合所构成的，并可用一个解析式表示的函数称为初等函数 cosx

yln(x 1x2

幂函数：ｙ＝

指数函数：ｙ＝

对数函数： （µ是常数） ； （ａ是常数，且ａ＞０,ａ≠１） ； （ａ是常数，且ａ＞０，ａ≠１） ；

三角函数 ：ｙ＝sinｘ，ｙ＝cosｘ，ｙ＝tanｘ，ｙ＝cotｘ，ｙ＝secｘ，ｙ＝cscｘ；

反三角函数：

正弦函数ｙ＝sinｘ在区间

［–

arcsinｘ.

余弦函数ｙ＝cosｘ在区间［０,

arccosｘ． ］上的反函数称为反正弦函数，记为ｙ＝]上的反函数称为反余弦函数，记为ｙ＝

正切函数ｙ＝tａnｘ在区间（–

为ｙ＝arctanｘ．

余切函数ｙ＝cotｘ在区间（０,

＝arccotｘ． ）上的反函数称为反正切函数，记)上的反函数称为反余切函数，记为ｙ

以上这五类函数统称为基本初等函数.由常数和基本初等函数经过有限次四则运算和有限次复合所产生的函数，称为初等函数

附：初等函数图像

极限教案(四)
函数与极限教案

第一章 函数与极限

教学目的：

1、理解函数的概念，掌握函数的表示方法，并会建立简单应用问题中的函数关

系式。

2、了解函数的奇偶性、单调性、周期性和有界性。

3、理解复合函数及分段函数的概念，了解反函数及隐函数的概念。

4、掌握基本初等函数的性质及其图形。

5、理解极限的概念，理解函数左极限与右极限的概念，以及极限存在与左、右

极限之间的关系。

6、掌握极限的性质及四则运算法则。

7、了解极限存在的两个准则，并会利用它们求极限，掌握利用两个重要极限求

极限的方法。

8、理解无穷小、无穷大的概念，掌握无穷小的比较方法，会用等价无穷小求极

限。

9、理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型。

10、了解连续函数的性质和初等函数的连续性，了解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理），并会应用这些性质。

教学重点：

1、 复合函数及分段函数的概念；

2、 基本初等函数的性质及其图形；

3、 极限的概念极限的性质及四则运算法则；

4、 两个重要极限；

5、 无穷小及无穷小的比较；

6、 函数连续性及初等函数的连续性；

7、 区间上连续函数的性质。

教学难点：

1、 分段函数的建立与性质；

2、 左极限与右极限概念及应用；

3、 极限存在的两个准则的应用；

4、 间断点及其分类；

5、 闭区间上连续函数性质的应用。

1. 1 映射与函数

一、集合

1. 集合概念

集合(简称集): 集合是指具有某种特定性质的事物的总体. 用A, B, C….等表示. 元素: 组成集合的事物称为集合的元素. a是集合M的元素表示为aM. 集合的表示:

列举法: 把集合的全体元素一一列举出来.

例如A{a, b, c, d, e, f, g}.

描述法: 若集合M是由元素具有某种性质P的元素x的全体所组成, 则M可表示为

A{a1, a2,   , an},

M{x | x具有性质P }.

例如M{(x, y)| x, y为实数, x2y21}.

几个数集:

N表示所有自然数构成的集合, 称为自然数集.

N{0, 1, 2, , n, }. N{1, 2, , n, }.

R表示所有实数构成的集合, 称为实数集.

Z表示所有整数构成的集合, 称为整数集.

Z{, n, , 2, 1, 0, 1, 2, , n, }.

Q表示所有有理数构成的集合, 称为有理数集.

Q{p

q|pZ,qN且p与q互质} 

子集: 若xA, 则必有xB, 则称A是B的子集, 记为AB(读作A包含于B)或BA .

如果集合A与集合B互为子集, AB且BA, 则称集合A与集合B相等, 记作AB.

 若AB且AB, 则称A是B的真子集, 记作AB . 例如, NZQR.

不含任何元素的集合称为空集, 记作. 规定空集是任何集合的子集.

2. 集合的运算

设A、B是两个集合, 由所有属于A或者属于B的元素组成的集合称为A与B的并集(简称并), 记作AB, 即

AB{x|xA或xB}.

设A、B是两个集合, 由所有既属于A又属于B的元素组成的集合称为A与B的交集(简称交), 记作AB, 即

AB{x|xA且xB}.

设A、B是两个集合, 由所有属于A而不属于B的元素组成的集合称为A与B的差集(简称差), 记作A\B, 即

A\B{x|xA且xB}.

如果我们研究某个问题限定在一个大的集合I中进行, 所研究的其他集合A都是I的子集. 此时, 我们称集合I为全集或基本集. 称I\A为A的余集或补集, 记作AC. 集合运算的法则:

设A、B、C为任意三个集合, 则

(1)交换律ABBA, ABBA;

(2)结合律 (AB)CA(BC), (AB)CA(BC);

(3)分配律 (AB)C(AC)(BC), (AB)C(AC)(BC);

(4)对偶律 (AB)CAC BC, (AB)CAC BC.

(AB)CAC BC的证明:

x(AB)CxABxA且xBxA C且xBC xAC BC, 所以(AB)CAC BC.

直积(笛卡儿乘积):

设A、B是任意两个集合, 在集合A中任意取一个元素x, 在集合B中任意取一个元素y, 组成一个有序对(x, y), 把这样的有序对作为新元素, 它们全体组成的集合称为集合A与集合B的直积, 记为AB, 即

AB{(x, y)|xA且yB}.

例如, RR{(x, y)| xR且yR }即为xOy面上全体点的集合, RR常记作R2.

3. 区间和邻域

有限区间:

设a<b, 称数集{x|a<x<b}为开区间, 记为(a, b), 即

(a, b){x|a<x<b}.

类似地有

[a, b]  {x | a xb }称为闭区间,

[a, b)  {x | ax<b }、(a, b]  {x | a<xb }称为半开区间.

其中a和b称为区间(a, b)、[a, b]、[a, b)、(a, b]的端点, ba称为区间的长度. 无限区间:

[a, )  {x | ax }, (, b]  {x | x < b } , (, ){x | | x | < }.

区间在数轴上的表示:

邻域: 以点a为中心的任何开区间称为点a的邻域, 记作U(a).

设是一正数, 则称开区间(a, a)为点a的邻域, 记作U(a, ), 即

U(a, ){x | a< x < a}

{x | | xa|<}.

其中点a称为邻域的中心,  称为邻域的半径.

去心邻域U(a, ):



U(a, ){x |0<| xa |<}

二、映射

1. 映射的概念

定义 设X、Y是两个非空集合, 如果存在一个法则f, 使得对X中每个元素x, 按法则f, 在Y中有唯一确定的元素y与之对应, 则称f为从X到Y的映射, 记作 f : XY ,

其中y称为元素x(在映射f下)的像, 并记作f(x), 即

yf(x),

而元素x称为元素y(在映射f下)的一个原像; 集合X称为映射f的定义域, 记作D f, 即 D fX ;

X中所有元素的像所组成的集合称为映射f的值域, 记为R f, 或f(X), 即

R ff(X){f(x)|xX}.

需要注意的问题:【极限教案】

(1)构成一个映射必须具备以下三个要素: 集合X, 即定义域D fX; 集合Y, 即值域的范围: R f Y; 对应法则f, 使对每个xX, 有唯一确定的yf(x)与之对应.

(2)对每个xX, 元素x的像y是唯一的; 而对每个yR f, 元素y的原像不一定是唯一的; 映射f的值域R f是Y的一个子集, 即R f Y, 不一定R fY .

例1设f : RR, 对每个xR, f(x)x2.

显然, f是一个映射, f的定义域D fR, 值域R f {y|y0}, 它是R的一个真子集. 对于R f 中的元素y, 除y0外, 它的原像不是唯一的. 如y4的原像就有x2和x2两个.

例2设X{(x, y)|x2y21}, Y{(x, 0)||x|1}, f : X Y, 对每个(x, y)X, 有唯一确定的(x, 0)Y与之对应.

显然f是一个映射, f的定义域D fX, 值域R f Y. 在几何上, 这个映射表示将平面上一个圆心在原点的单位圆周上的点投影到x轴的区间[1, 1]上.

(3) f :[

2, 2][1, 1], 对每个x[



2, 2], 2, 2], f(x)sin x . f是一个映射, 定义域D f [值域R f [1, 1].

满射、单射和双射:

设f是从集合X到集合Y的映射, 若R f Y, 即Y中任一元素y都是X中某元素的像, 则称f为X到Y上的映射或满射; 若对X中任意两个不同元素x 1x 2, 它们的像f(x 1)f(x 2), 则称f为X到Y的单射; 若映射f既是单射, 又是满射, 则称f为一一映射(或双射).

上述三例各是什么映射？

2. 逆映射与复合映射

设f是X到Y的单射, 则由定义, 对每个yR f , 有唯一的xX, 适合f(x)y, 于是, 我们可定义一个从R f 到X的新映射g, 即

g : R f X,

对每个yR f , 规定g(y)x, 这x满足f(x)y. 这个映射g称为f的逆映射, 记作f 1, 其定义域DfR f , 值域RfX . 11

按上述定义, 只有单射才存在逆映射. 上述三例中哪个映射存在逆映射？ 设有两个映射

g : XY 1, f : Y 2Z,

其中Y 1Y 2. 则由映射g和f可以定出一个从X到Z的对应法则, 它将每个xX映射成f[g(x)]Z . 显然, 这个对应法则确定了一个从X到Z的映射, 这个映射称为映射g和f构成的复合映射, 记作f o g, 即

f o g: X Z,

(f o g)(x)f[g(x)], xX .

应注意的问题:

映射g和f构成复合映射的条件是: g的值域R g必须包含在f的定义域内, R gD f . 否则, 不能构成复合映射. 由此可以知道, 映射g和f的复合是有顺序的, f o g有意义并不表示g o f也有意义. 即使f o g与g o f都有意义, 复映射f o g与g o f也未必相同.

例4 设有映射g : R[1, 1], 对每个xR, g(x)sin x,

映射f : [1, 1][0, 1], 对每个u[1, 1], f(u)u2.

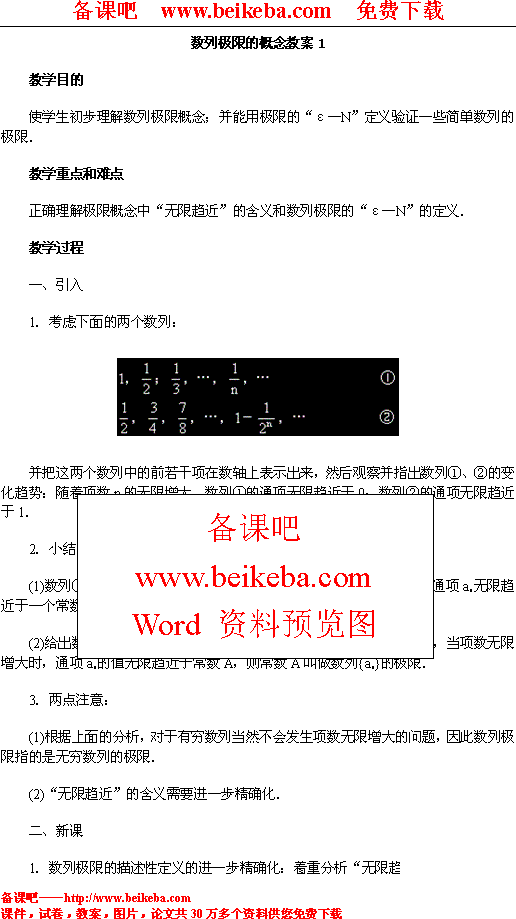
则映射g和f构成复映射f o g: R[0, 1], 对每个xR, 有

(fg)(x)f[g(x)]f(sixn)sinx|cosx|. 2

三、函数

1. 函数概念

定义 设数集DR, 则称映射f : D R为定义在D上的函数, 通常简记为 yf(x), xD,

极限教案(五)
高数函数与极限教案

授课时间： 20 年9月 日 使用班级：

授课时间： 20 年9月 日 使用班级：

授课章节名称：

第1章 函数、极限与连续

第1节 函数（二）、第2节 极限

教学目的：

1.理解复合函数的定义及复合过程，分段函数的定义及表示方法，极限的概念，函数左极限与右极限的概念；

2.熟练掌握x和xx0时f(x)的极限存在的充要条件；

3.理解无穷大、无穷小的概念；

4.掌握无穷大的判定方法和无穷小的概念及性质，会用无穷小量的性质求教学重点：

1.函数极限与数列极限的概念，求极限的方法；

2.无穷大量与无穷小量的概念及性质.

教学难点：

1.函数极限的定义；

2.无穷大量与无穷小量的概念和性质及其应用。

教学方法：讲授，启发式、讲练结合

教学手段：传统讲授。

作业：

层次1：书16页1、2（1）（2）、4、6

层次2：书16页5、7

教案实施效果追记：

（手书）

第1章 函数、极限与连续

第1节 函数（二）、第2节 极限

复习及课题引入（时间：5分钟）：

1、作业题处理；

2、复习函数的相关性质以及基本初等函数的相关知识点。

讲授新内容

※※※※

一、函数的概念（二）（时间：15分钟）

1、复合函数：

【引例】（公司员工问题）

某公司员工的工资占公司利润的若干比例，而公司的利润又取决于所销售的商品的数量，因此，该公司员工的工资由所销售商品的数量决定。

定义7设yfu,其中ux,且函数ux的值域包含在函

数yfu的定义域内,则称yfx为由yfu与ux复合而成的复合函数,其中u称为中间变量.

例如，yu,usinx可复合成ysin22x.

注意：

①、并不是任意两个函数都能构成复合函数.

如，yu2和ux22就不能构成复合函数。因为对函数yu2而言，必须要求变量u1，而ux222，所以对任何x的1，

值，y都得不到确定的对应值。

②、利用复合函数不仅能将若干个简单的函数复合成一个函数，还可以把一个较复杂的函数分解成几个简单的函数，这对于今后掌握微积分的运算时很重要的。

例4、将下列复合函数进行分解.

(1)ylncosx; (2)ysinx.

解 (1)ylncosx是由ylnu,ucosx复合而成的. (2)yx是由yu,usinx复合而成的.

2、初等函数：

定义8：由基本初等函数经过有限次的四则运算和有限次的复合步骤所构成并用一个式子表示的函数，称为初等函数.

x(xx21)例如：ylncosx，y，ycos2x2等都是初等函数。 x1

3、分段函数：

定义9：在自变量的不同变化范围中，对应法则用不同式子表示的函数，称为分段函数.

注:

(1)分段函数仍旧是一个函数，而不是几个函数，分段函数的定义域是各段函数定义域的并集.

x,x0, (2)分段函数一般不是初等函数.除yx x,x0,

例如：

x0,1,sgnx0, x0,就是一个分段函数，其定义域为(,)。

1,x0,

2x,-1x0,1例5、设y1x,，0x1,求f0,f,f2及函数的定义域。 21,1x3

111解：f020,f1,f21，函数的定义域为(1,3)。 222

※※※※

二、极限概念：（时间：10分钟）

【引例】：

中国古代哲学家庄周在《庄子•天下篇》中引述惠施的话：“一尺之锤，日取一半，万世不竭。”

1析：这句话的意思是指一尺的木棒，第一天取它的一半，即尺，；第2

11二天再取剩下的一半，即尺；第三天再取第二天剩下的一半，即尺；这48

样一天天地去下去，而木棒是永远也取不完的。

尽管木棒永远也取不完，可到了一定的时候，还能看得见吗？看不见意味着什么？不就是快没了吗？终极的时候，就近乎没有了。它的终极状态就趋于零。

【极限概念引出】事实上，假设木棒为一个单位长，用xn表示第n天截取之后所剩下的长度，可得x11111,x2,x3,...,xnn,..., 2482

，这样x1,x2,x3,...,xn,...构成一列有次序的数。设想n无限增大（记为

，在这个过程中，xn无限接近于一个确定的数值（零），这个确定的n）

数值在数学上称为上面这列有次序的数（所谓数列），x1,x2,x3,...,xn,...当n时的极限。 复习(高中知识)：数列的概念、通项概念

数列就是按照一定顺序排列成的一列数，一般记为x1,x2,x3,...,xn,...，简记为{xn}，其中xn称为数列的通项。

例如，数列1,2,3,4,5，„的通项是xnn，可以记为{n}；数列1111111,,,,,...的通项是xn，可以记为{}；数列2,22,23,24,25,...,的通项2345nn

是xn2n，可以记为{2n}。

数列{xn}也可看成自变量为正整数n的函数：xnfn，其定义域是全体正整数，当自变量n依次取1,2,3,，„一切正整数时，对应的函数值就排列成数列{xn}。

2、（极限概念）定义10：（教学方法：板书）

对于数列{xn},若当n无限增大时,通项xn无限接近于某个确定的常数则常数A,A称为数列{xn}的极限,此时也称数列{xn}收敛于A,

记为nlimxnA或xnAn

若数列{xn}的极限不存在,则称数列{xn}发散.

注意：数列极限是个动态概念，是变量无线运动渐进变化的过程，是一个变量（项数为n）无线运动的同时另一个变量（对应的通项{xn}）无限接近于某一个确定常数的过程，这个常数（极限）是这个无线运动变化的最终趋势。（根据函数关系的定义，引出数列是特殊的函数这个概念）

例1、（画数轴数形结合思想）

3456n1n1:2,,,,,...,,...； （1）xnn2345n

111111（2）xnn:,,,,...,n,...； 33392781

（3）xn1:1,1,1,1,...,1,...； nn

解：当时n，数列（1）的通项xn

的通项xnn1越来越接近于常数1；而数列（2）n1nx1越来越接近于常数0，数列（3）的通项在-1与1之间n3n

交替出现而不趋于任何确定的常数，所以，

n1（1）lim1； nn

1（2）limn0； n3

（3）lim1不存在。（析：从数轴上标出一些点，来说明数列无限运动变n

n

化的最终趋势）

※※※※

三、函数的极限（时间：20分钟）

数列是一种特殊形式的函数，把数列的极限推广可得到函数的极限。根据自变量的变化过程，分两种情况讨论。

1、x时函数fx的极限（教学方法：讲解）（7分钟）

【引例】（设备折旧问题）

某高校为进行以工作过程为导向的课程教学，购置一批数控机床为教学设备，投资额是100万元，每年的折旧费为这批数控机床账面价格（即以前各年折1旧费用提取后余下的价格），那么这批数控机床的账面价格（单位：万元）10

99293第一年为100，第二年为100*，第三年为100*，第四年为100*，„,（）（）101010

9n第n年为100*，那么，当n无限增大时，该批数控机床的账面价格如何变（）10

化？

显然，从它的变化趋势可以看出，随着年数的无限增大时，账面价格无限接近于0.

引例反映了一个特点：当自变量逐渐增大时，相应的函数值逐渐接近于一个确定的常数。为此给出下面定义。

x定义11：函数yf(x) 在(,) 内有定义，若 无限增大时，相应的

函数值f(x) 无限接近于一个确定的常数A，则称函数f(x) 以A为极限。记为limf(x)x=A或f(x)A（x ）.

若当x （或x ）时，函数无限接近于一个确定的常数A，记为xlimf(x)limf(x)x=A或=A. 1110,lim0,lim0,xxxx例如，xx （画出图形解释） lim

不难证明，函数f(x) 在x 时的极限与在x，x时的极限有以下关系。

定理1：limf(x)Alimf(x)limf(x)A xxx

例2、（书16页3）

讨论limex 是否存在。（根据函数图像观察） x

2、xx0时函数fx的极限（13分钟）

（1）邻域概念：

以上就是中国招生考试网http://www.chinazhaokao.com/带给大家不一样的精彩成考报名。想要了解更多《极限教案》的朋友可以持续关注中国招生考试网，我们将会为你奉上最全最新鲜的成考报名内容哦! 中国招生考试网，因你而精彩。

相关热词搜索：函数的极限教案 数列的极限教案