导读: 圆锥曲线高考题分享,下面是中国招生考试网http: www chinazhaokao com 小编今天为大家精心准备了圆锥曲线高考题,希望对大家有所帮助 ...
圆锥曲线高考题(一)
(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))椭圆 的左、右焦点分别是 ,离心率为 ,过 且垂直于 轴的直线被椭圆 截得的线段长为1.
(Ⅰ)求椭圆 的方程;
(Ⅱ)点 是椭圆 上除长轴端点外的任一点,连接 ,设 的角平分线 交 的长轴于点 ,求 的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过 点作斜率为 的直线 ,使得 与椭圆 有且只有一个公共点,设直线 的斜率分别为 ,若 ,试证明 为定值,并求出这个定值.
【答案】解:(Ⅰ)由于 ,将 代入椭圆方程 得
由题意知 ,即 又
所以 , 所以椭圆方程为
(Ⅱ)由题意可知: = , = ,设 其中 ,将向量坐标代入并化简得:m( ,因为 ,
所以 ,而 ,所以
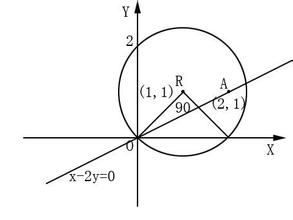
(3)由题意可知,l为椭圆的在p点处的切线,由导数法可求得,切线方程为:
,所以 ,而 ,代入 中得
为定值.
33.(2013年高考上海卷(理))(3分+5分+8分)如图,已知曲线 ,曲线 ,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
(1)在正确证明 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与 有公共点,求证 ,进而证明原点不是“C1—C2型点”;
(3)求证:圆 内的点都不是“C1—C2型点”.
【答案】:(1)C1的左焦点为 ,过F的直线 与C1交于 ,与C2交 于 ,故C1的左焦点为“C1-C2型点”,且直线可以为 ;
(2)直线 与C2有交点,则
,若方程组有解,则必须 ;
直线 与C2有交点,则
,若方程组有解,则必须
故直线 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”.
(3)显然过圆 内一点的直线 若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线 斜率存 在且与曲线C2交于点 ,则
直线 与圆 内部有交点,故
化 简得, ............①
若直线 与曲线C1有交点,则
化简得, .....②
由①②得,
但此时,因为 ,即①式不成立;
当 时,①式也不成立
综上, 直线 若与圆 内有交点,则不可能同时与曲线C1和C2有交点,
即圆 内的点都不是“C1-C2型点” .
34.(2013年普通高等学校招生统一考试福建数学(理)试题(纯WORD版))如图,在正方形 中, 为坐标原点,点 的坐标为 ,点 的坐标为 .分别将线段 和 十等分,分点分别记为 和 ,连结 ,过 做 轴的垂线与 交于点 .
(1)求证:点 都在同一条抛物线上,并求该抛物线 的方程;
(2)过点 做直线与抛物线 交于不同的两点 ,若 与 的面积比为 ,求直线的方程.
【答案】解:(Ⅰ)依题意,过 且与x轴垂直的直线方程为
, 直线 的方程为
设 坐标为 ,由 得: ,即 ,
都在同一条抛物线上,且抛物线 方程为
(Ⅱ)依题意:直线的斜率存在,设直线的方程为
由 得
此时 ,直线与抛物线 恒有两个不同的交点
设: ,则
又 ,
分别带入 ,解得
直线的方程为 ,即 或
35.(2013年高考湖南卷(理))过抛物线 的焦点F作斜 率分别为 的两条不同的直线 ,且 , 相交于点A,B, 相交于点C,D.以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为 .
(I)若 ,证明; ;
(II)若点M到直线 的距离的最小值为 ,求抛物线E的方程.
36.(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))如图,点 是椭圆 的一个顶点, 的长轴是圆 的直径. 是过点 且互相垂直的两条直线,其中 交圆 于两点, 交椭圆 于另一点
(1)求椭圆 的方程; (2)求 面积取最大值时直线 的方程.
【答案】解:(Ⅰ)由已知得到 ,且 ,所以椭圆的方程是 ;
(Ⅱ)因为直线 ,且都过点 ,所以设直线 ,直线 ,所以圆心 到直线 的距离为 ,所以直线 被圆 所截的弦 ;
由 ,所以
,所以
,
当 时等号成立,此时直线
37.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))如题(21)图,椭圆的中心为原点 ,长轴在 轴上,离心率 ,过左焦点 作 轴的垂线交椭圆于 两点, .
(1)求该椭圆的标准方程;
(2)取垂直于 轴的直线与椭圆相交于不同的两点 ,过 作圆心为 的圆,使椭圆上的其余点均在圆 外.若 ,求圆 的标准方程.
38.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))设椭圆 的焦点在 轴上
(Ⅰ)若椭圆 的焦距为1,求椭圆 的方程;
(Ⅱ)设 分别是椭圆的左、右焦点, 为椭圆 上的第一象限内的点,直线 交 轴与点 ,并且 ,证明:当 变化时,点 在某定直线上.
【答案】解: (Ⅰ) .
(Ⅱ) .
由 .
所以动点P过定直线 .
39.(2013年高考新课标1(理))已知圆 : ,圆 : ,动圆 与 外切并且与圆 内切,圆心 的轨迹为曲线 C.
(Ⅰ)求C的方程;
(Ⅱ) 是与圆 ,圆 都相切的一条直线, 与曲线C交于A,B两点,当 圆P的半径最长时,求|AB|.
【答案】由已知得圆 的圆心为 (-1,0),半径 =1,圆 的圆心为 (1,0),半径 =3.
设动圆 的圆心为 ( , ),半径为R. [来源:www.5ykj.Com]
(Ⅰ)∵圆 与圆 外切且与圆 内切,∴|PM|+|PN|= = =4,
由椭圆的定义可知,曲线C是以M,N为左右焦点,场半轴长为2,短半轴长为 的椭圆(左顶点除外),其方程为 .
(Ⅱ)对于曲线C上任意一点 ( , ),由于|PM|-|PN|= ≤2,∴R≤2,
当且仅当圆P的圆心为(2,0)时,R=2.
∴当圆P的半径最长时,其方程为 ,
当 的倾斜角为 时,则 与 轴重合,可得|AB|= .
当 的倾斜角不为 时,由 ≠R知 不平行 轴,设 与 轴的交点为Q,则 = ,可求得Q(-4,0),∴设 : ,由 于圆M相切得 ,解得 .
当 = 时,将 代入 并整理得 ,解得 = ,∴|AB|= = .
当 =- 时,由图形的对称性可知|AB|= ,
综上,|AB|= 或|AB|= .
40.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))设椭圆 的左焦点为F, 离心率为 , 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设A, B分别为椭圆的左右顶点, 过点F且斜率为k的直线与椭圆交于C, D两点. 若 , 求k的值.
【答案】
41.(2013年高考江西卷(理))如图,椭圆 经过点 离心率 ,直线 的方程为 .
(1) 求椭圆 的方程;
(2) 是经过右焦点 的任一弦(不经过点 ),设直线 与直线 相交于点 ,记 的斜率分别为 问:是否存在常数 ,使得 ?若存在求 的值;若不存在,说明理由.
【答案】解:(1)由 在椭圆上得, ①
依题设知 ,则 ②
②代入①解得 .
故椭圆 的方程为 .
(2)方法一:由题意可设 的斜率为 ,
则直线 的方程为 ③
代入椭圆方程 并整理,得 ,
设 ,则有
④
在方程③中令 得, 的坐标为 .
从而 .
注意到 共线,则有 ,即有 .
所以
⑤
④代入⑤得 ,
又 ,所以 .故存在常数 符合题意.
方法二:设 ,则直线 的方程为: ,
令 ,求得 ,
从而直线 的斜率为 ,
联立 ,得 ,
则直线 的斜率为: ,直线 的斜率为: ,
所以 ,
故存在常数 符合题意.
42.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD版))已知抛物线 的顶点为原点,其焦点 到直线 : 的距离为 .设 为直线 上的点,过点 作抛物线 的两条切线 ,其中 为切点.
(Ⅰ) 求抛物线 的方程;
(Ⅱ) 当点 为直线 上的定点时,求直线 的方程;
(Ⅲ) 当点 在直线 上移动时,求 的最小值.
【答案】(Ⅰ) 依题意,设抛物线 的方程为 ,由 结合 ,解得 .
所以抛物线 的方程为 .
(Ⅱ) 抛物线 的方程为 ,即 ,求导得
设 , (其中 ),则切线 的斜率分别为 , ,
所以切线 的方程为 ,即 ,即
同理可得切线 的方程为
因为切线 均过点 ,所以 ,
所以 为方程 的两组解.
所以直线 的方程为 .
(Ⅲ) 由抛物线定义可知 , ,
所以
联立方程 ,消去 整理得
由一元二次方程根与系数的关系可得 ,
所以
又点 在直线 上,所以 ,
所以
所以当 时, 取得最小值,且最小值为 .
43.(2013年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD版含答案))平面直角坐标系 中,过椭圆 的右焦点 作直 交 于 两点, 为 的中点,且 的斜率为 .
(Ⅰ)求 的方程;
(Ⅱ) 为 上的两点,若四边形 的对角线 ,求四边形 面积的最大值.
【答案】
44.(2013年高考湖北卷(理))如图,已知椭圆 与 的中心在坐标原点 ,长轴均为 且在 轴上,短轴长分别为 , ,过原点且不与 轴重合的直线 与 , 的四个交点按纵坐标从大到小依次为 , , , .记 , 和 的面积分别为 和 .
(I)当直线 与 轴重合时,若 ,求 的值;
(II)当 变化时,是否存在与坐标轴不重合的直线 ,使得 ?并说明理由.
【答案】解:(I) ,
解得: (舍去小于1的根)
(II)设椭圆 , ,直线 :
同理可得,
又 和 的的高相等
如果存在非零实数 使得 ,则有 ,
即: ,解得
当 时, ,存在这样的直线 ;当 时, ,不存在这样的直线 .
45.(2013年高考北京卷(理))已知A、B、C是椭圆W: 上的三个点,O是坐标原点.
(I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
【答案】解:(I)椭圆W: 的右顶点B的坐标为(2,0).因为四边形OABC为菱形,所以AC与OB相互垂直平分. 所以可设A(1, ),代入椭圆方程得 ,即 . 所以菱形OABC的面积是 .
(II)假设四边形OABC为菱形. 因为点B不是W的顶点,且直线AC不过原点,所以可设AC的方程为 .
由 消去 并整理得 .
设A ,C ,则 , .
所以AC的中点为M( , ).
因为M为AC和OB的交点,所以直线OB的斜率为 .
因为 ,所以AC与OB不垂直. 所以OABC不是菱形,与假设矛盾.
所以当点B不是W的顶点时,四边形OABC不可能是菱形.
46.(2013年高考陕西卷(理))已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(Ⅰ) 求动圆圆心的轨迹C的方程;
(Ⅱ) 已知点B(-1,0), 设不垂直于x轴的直线 与轨迹C交于不同的两点P, Q, 若x轴是 的角平分线, 证明直线 过定点.
【答案】解:(Ⅰ) A(4,0),设圆心C
(Ⅱ) 点B(-1,0), .
直线PQ方程为:
所以,直线PQ过定点(1,0)
47.(2013年普通高等学校招生统一考试辽宁数 学(理)试题(WORD版))如图,抛物线 ,点 在抛物线 上,过 作 的切线,切点为 ( 为原点 时, 重合于 ) ,切线 的斜率为 .
(I)求 的值;
(II)当 在 上运动时,求线段 中点 的轨迹方程.
【答案】
48.(2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答案(已校对))已知双曲线 的左、右焦点分别为 ,离心率为 直线 与 的两个交点间的距离为 .
(I)求 ;
(II)设过 的直线 与 的左、右两支分别相交于 两点,且 ,证明: 成等比数列.
【答案】
49.(2013年上海市春季高考数学试卷(含答案))本题共有2个小题,第1小题满分6分,第2小题满分6分.
已知抛物线 的焦点为 .
(1)点 满足 .当点 在抛物线 上运动时,求动点 的轨迹方程;
(2)在 轴上是否存在点 ,使得点 关于直线 的对称点在抛物线 上?如果存在,求所有满足条件的点 的坐标;如果不存在,请说明理由.
【答案】(1)设动点 的坐标为 ,点 的坐标为 ,则 ,
因为 的坐标为 ,所以 ,
由 得 .
即 解得
代入 ,得到动点 的轨迹方程为 .
(2)设点 的坐标为 .点 关于直线 的对称点为 ,
则 解得
若 在 上,将 的坐标代入 ,得 ,即 或 .
所以存在满足题意的点 ,其坐标为 和 .
圆锥曲线高考题(二)
1.(2014山东青岛高三第一次模拟考试, 10) 如图,从点 发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点 ,经抛物线反射后,穿过焦点射向抛物线上的点 ,再经抛物线反射后射向直线 上的点 ,经直线反射后又回到点 ,则 等于( )
A. B. C. D.
[答案] 1. B
[解析] 1.由题意可得抛物线的轴为 轴, ,所以 所在的直线方程为 ,
在抛物线方程 中,令 可得 ,即
从而可得 , ,
因为经抛物线反射后射向直线 上的点 ,经直线反射后又回到点 ,
所以直线 的方程为 ,
故选B.
2.(2014安徽合肥高三第二次质量检测,4) 下列双曲线中,有一个焦点在抛物线 准线上的是( )
A. B.
C. D.
[答案] 2. D
[解析] 2. 因为抛物线 的焦点坐标为 ,准线方程为 ,所以双曲线的焦点在 轴
上,双曲线 的焦点在 轴且为 满足条件. 故选D.
3. (2014贵州贵阳高三适应性监测考试, 10) 在平面直角坐标系 中,抛物线 : 的焦点为 , 是抛物线 上的点,若 的外接圆与抛物线 的准线相切,且该圆面积 ,则 ( )
A. 2 B. 4 C. 6 D. 8
[答案] 3.B
[解析] 3.因为 的中垂线 过外接圆圆心,所以此直线与准线 的距离即为外接圆半径,故 = ,故 .
4. (2014北京东城高三第二学期教学检测,7) 已知抛物线 : 的焦点与双曲线 : 的右焦点的连线交 于第一象限的点 , 若 在点 处的切线平行于 的一条渐近线,则 ( )
A.
B.
C.
D.
[答案] 4.D
[解析] 4. 由已知可得抛物线的焦点 ,双曲线的右焦点为 ,两个点连线的直线方程为 。设该直线与抛物线于 ,则 在 处的切线的斜率为 ,由题意知 ,所以 ,所 以 ,代入直线方程可解得
5.(2014山东潍坊高三3月模拟考试数学(理)试题,10)如图,已知直线l:y=k(x+1) (k> 0) 与抛物线C:y2=4x相交于A、B两点,且A、B两点在抛物线C准线上的射影分别是M、N,若|AM|=2|BN|,则k的值是( )
(A) (B) (C) (D) 2
[答案] 5. C
[解析] 5. 设点 ,则由抛物线的定义可得 ,整理得 ①.
联立直线与抛物线方程得 ,根据根与系数的关系,可得 ,与①联立得 , ,所以点 ,其斜率为 .
6.(2014江西重点中学协作体高三第一次联考数学(理)试题,10)给定圆 : 及抛物线 : 过圆心 作直线 , 此直线与上述两曲线的四个交点, 自上而下顺次记为 如果线段 的长按此顺序构成一个等差数列, 则直线 的斜率为( )
A. B. C. D.
[答案] 6. C
[解析] 6. 圆P的圆心P(1,0),抛物线的焦点坐标为(1,0). 由圆P与抛物线的位置关系可得,点A和点D在抛物线上,点B和点C在圆上,因为直线l过圆心,可得BC=2,又因为 的长按此顺序构成一个等差数列可得 ,设点 ,根据抛物线的定义可知 ,可得 . 显然直线l的斜率存在,设直线方程为 ,联立直线与抛物线方程可得 ,解得 .
7.(2014吉林实验中学高三年级第一次模拟,11)中心在原点,焦点在 轴上的双曲线 的离心率为2,直线 与双曲线 交于 两点,线段 中点 在第一象限,并且在抛物线 上,且 到抛物线焦点的距离为 ,则直线 的斜率为( )
A. B. C. D.
[答案] 7. C
[解析] 7. 根据题意可设双曲线的方程为 . 根据抛物线的定义可得点M( ),设点 ,则 、 ,两式相减得 ,因为 ,则得 ,即直线l的斜率为 .
8.(2014吉林实验中学高三年级第一次模拟,9)若抛物线 的焦点是F,准线是 ,点M(4,4)是抛物线上一点,则经过点F、M且与 相切的圆共有( )
A.0个 B.1个 C.2个 D.4个
[答案] 8. C
[解析] 8. 焦点F的坐标为(1,0),准线为x=-1,由圆与 相切可设圆的方程为: ,则由题意可得 ①、 ②两式联立得 ,代入到①中消b得关于a的一元二次方程,此方程有两个实数根,由此可得此圆共有2个.
9. (2014重庆五区高三第一次学生调研抽测,8) 设 为抛物线 的焦点, 为该抛物线上三点,若 ,则 的值为 ( )
A. B. C. D. 12
[答案] 9. B
[解析] 9. 由 得 .
所以 . 选B.
10.(2014湖北八市高三下学期3月联考,9) 己知抛物线 的焦点F恰好是双曲线 的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为( )
A. +1 B.2 C. D. -1
[答案] 10. A
[解析] 10. 由题意得抛物线上的点 在双曲线上,而 ,所以点 在双曲线上,因此 又因为 ,所以 .
11. (2014湖南株洲高三教学质量检测(一),6) 在同一坐标系中,离心率为 的椭圆与离心率为 的双曲线有相同的焦点 ,椭圆与双曲线的一个交点与两焦点 的连线互相垂直,则 ( )
(A) 2 (B)3 (C) (D)
[答案] 11. A
[解析] 11. 依题意,设焦距为 ,椭圆长轴长 ,双曲线实轴长 ,令点 在上去先的右支上,
由椭圆的定义知 ,①
由双曲线的定义知 ,②
又 , ,
由① ② 得 ,
,即 ,故 .
12. (2 014天津七校高三联考, 6) 以抛物线 的焦点为圆心,且与双曲线 的渐近线相切的圆的方程为( )
(A) (B)
(C) (D)
[答案] 12. D
[解析] 12. 由双曲线方程知 ,实轴长为6,离心率 ,右焦点坐标 ,即圆心的坐
标,渐近线方程为 ,圆心到渐近线 的距离为 ,即圆的半径为4,
故所求的圆的方程为 .
13. (2014河南郑州高中毕业班第一次质量预测, 8) 已知抛物线 ,过其焦点且斜率为 的直线交抛物线于 , 两点,若线段 的中点的横坐标为3,则该抛物线的准线方程为 ( )
A.
B.
C.
D.
[答案] 13. C
[解析] 13.设 ,由于直线过焦点且斜率为 ,则其方程为 ,
联立方程组 ,消去 得 , , .
故抛物线的准线方程为 .
14. (2014湖北黄冈高三期末考试) 已知双曲线 的两条渐近线与抛物线 的准线分别交于 、 两点, 为坐标原点, 的面积为 ,则双曲线 的离心率 ( )
A.
B.
C.
D.
[答案] 14. C
[解析] 14.双曲线的性质. 双曲线的渐近线方程为 ,准线方程为 ,又 ,即 , ,解得 .
15. (2014北京东城高三12月教学质量调研) 设F为抛物线 的焦点, 、 、 为该抛物线上三点,若 ,则 的值为( )
(A)3 (B)4 (C)6 (D)9
[答案] 15. C
[解析] 15. 由题意可得 ,点 时抛物线的焦点,也是三角形 的重心,故 ,
,再由抛物线的定义可得 .
16. (2014湖南,15,5分)如图,正方形ABCD和正方形DEFG的边长分别为a,b(a<b),原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则 =________.
[答案] 16.1+
[解析] 16.|OD|= ,|DE|=b,|DC|=a,|EF|=b,
故C ,F ,
又抛物线y2=2px(p>0)经过C、F两点,
从而有 即
∴b2=a2+2ab,∴ -2• -1=0,
又 >1,
∴ =1+ .
17. (2014天津蓟县第二中学高三第一次模拟考试,12) 抛物线 +12y=0的准线方程是___________.
[答案] 17. y=3
[解析] 17. 抛物线的标准方程为: ,由此可以判断焦点在y轴上,且开口向下,且p=6,所以其准线方程为y=3.
18. (2014河北唐山高三第一次模拟考试,15) 过抛物线 : 的焦点 作直线 交抛物线 于 、 两点,若 到抛物线的准线的距离为4,则 ________________.
[答案] 18.
[解析] 18. 设 ,由抛物线的性质: ,所以 ,又 ,
所以 ,从而 .
19. (2014河北衡水中学高三上学期第五次调研考试, 15) 已知抛物线 到其焦点的距离为5,双曲线 的左顶点为A,若双曲线一条渐近线与直线 垂直,则实数 _________.
[答案] 19.
[解析] 19.由已知可得 ,从而 . 因为 ,所以 ,从而渐近线的斜率为 ,故 ,得 .
20. (2014兰州高三第一次诊断考试, 15) 如图,过抛物线 的焦点F的直线 依次交抛物线及其准线于点A、B、C,
若|BC|=2|BF|,且|AF|=3,则抛物线的方程是 .
[答案] 20.
[解析] 20. 如图,分别过点 、 作准线的垂线,分别交准线于 、 ,设 ,则由已知得 ,由抛物线的定义知 ,故 ,
在直角三角形 中, ,
, ,即 ,
又 , ,即 ,
故所 求抛物线方程为 .
21. (2014大纲全国,21,12分)已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且|QF|= |PQ|.
(Ⅰ)求C的方程;
(Ⅱ)过F的直线l与C相交于A、B两点,若AB的垂直平分线l'与C相交于M、N两点,且A、M、B、N四点在同一圆上,求l的方程.
[答案] 21.查看解析
[解析] 21.(Ⅰ)设Q(x0,4),代入y2=2px得x0= .
所以|PQ|= ,|QF|= +x0= + .
由题设得 + = × ,解得p=-2(舍去)或p=2.
所以C的方程为y2=4x.(5分)
(Ⅱ)依题意知l与坐标轴不垂直,故可设l的方程为x=my+1(m≠0).
代入y2=4x得y2-4my-4=0.
设A(x1,y1),B(x2,y2),则y1+y2=4m,y1y2=-4.
故AB的中点为D(2m2+1,2m),|AB|= |y1-y2|=4(m2+1).
又l'的斜率为-m,所以l'的方程为x=- y+2m2+3.
将上式代入y2=4x,并整理得y2+ y-4(2m2+3)=0.
设M(x3,y3),N(x4,y4),则y3+y4=- ,y3y4=-4(2m2+3).
故MN的中点为E ,|MN|= |y3-y4|= .(10分)
由于MN垂直平分AB,故A、M、B、N四点在同一圆上等价于|AE|=|BE|= |MN|,从而 |AB|2+|DE|2= |MN|2,
即4(m2+1)2+ + = .
化简得m2-1=0,解得m=1或m=-1.
所求直线l的方程为x-y-1=0或x+y-1=0.(12分)
22. (2014陕 西,2017,13分)如图,曲线C由上半椭圆C1: + =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 .
(Ⅰ)求a,b的值;
(Ⅱ)过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
[答案] 22.查看解析
[解析] 22.(Ⅰ)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半椭圆C1的左,右顶点.
设C1的半焦距为c,由 = 及a2-c2=b2=1得a=2.
∴a=2,b=1.
(Ⅱ)解法一:由(Ⅰ)知,上半椭圆C1的方程为 +x2=1(y≥0).
易知,直线l与x轴不重合也不垂直,设其方程为y=k(x-1)(k≠0),
代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0.(*)
设点P的坐标为(xP,yP),
∵直线l过点B,∴x=1是方程(*)的一个根.
由求根公式,得xP= ,从而yP= ,
∴点P的坐标为 .
同理,由 得点Q的坐标为(-k-1,-k2-2k).
∴ = (k,-4), =-k(1,k+2).
∵AP⊥AQ,∴ • =0,即 [k-4(k+2)]=0,
∵k≠0,∴k-4(k+2)=0,解得k=- .
经检验,k=- 符合题意,
故直线l的方程为y=- (x-1).
解法二:若设直线l的方程为x=my+1(m≠0),比照解法一给分.
23.(2014安徽,19,1 3分)如图,已知两条抛物线E1:y2=2p1x(p1>0)和E2:y2=2p2x(p2>0),过原点O的两条直线l1和l2,l1与E1,E2分别交于A1,A2两点,l2与E1,E2分别交于B1,B2两点.
(Ⅰ)证明:A1B1∥A2B2;
(Ⅱ)过O作直线l(异于l1,l2)与E1,E2分别交于C1,C2两点.记△A1B1C1与△A2B2C2的面积分别为S1与S2,求 的值.
[答案] 23.查看解析
[解析] 23.(Ⅰ)证明:设直线l1,l2的方程分别为y=k1x,y=k2x(k1,k2≠0),则
由 得A1 ,
由 得A2 .
同理可得B1 ,B2 .
所以 = =2p1 ,
= =2p2 ,
故 = ,所以A1B1∥A2B2.
(Ⅱ)由(Ⅰ)知A1B1∥A2B2,同理可得B1C1∥B2C2,C1A1∥C2A2.
所以△A1B1C1∽△A2B2C2.
因此 = .
又由(Ⅰ)中的 = 知 = .
故 = .
24.(2014山东,21,14分)已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有|FA|=|FD|.当点A的横坐标为3时,△ADF为正三角形.
(Ⅰ)求C的方程;
(Ⅱ)若直线l1∥l,且l1和C有且只有一个公共点E,
(i)证明直线AE过定点,并求出定点坐标;
(ii)△ABE的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
[答案] 24.查看解析
[解析] 24.(Ⅰ)由题意知F .
设D(t,0)(t>0),则FD的中点为 .
因为|FA|=|FD|,
由抛物线的定义知3+ = ,
解得t=3+p或t=-3(舍去).
由 =3,解得p=2.
所以抛物线C的方程为y2=4x.
(Ⅱ)(i)由(Ⅰ)知F(1,0),
设A(x0,y0)(x0y0≠0),D(xD,0)(xD>0),
因为|FA|=|FD|,则|xD-1|=x0+1,
由xD>0得xD=x0+2,故D(x0+2,0).
故直线AB的斜率kAB=- .
因为直线l1和直线AB平行,
设直线l1的方程为y=- x+b,
代入抛物线方程得y2+ y- =0,
由题意Δ= + =0,得b=- .
设E(xE,yE),则yE=- ,xE= ,
当 ≠4时,kAE= =- = ,
可得直线AE的方程为y-y0= (x-x0),
由 =4x0,
整理可得y= (x-1),
直线AE恒过点F(1,0).
当 =4时,直线AE的方程为x=1,过点F(1,0),
所以直线AE过定点F(1,0).
(ii)由(i)知直线AE过焦点F(1,0),
所以|AE|=|AF|+|FE|=(x0+1)+ =x0+ +2.
设直线AE的方程为x=my+1,
因为点A(x0,y0)在直线AE上,
故m= ,
设B(x1,y1),
直线AB的方程为y-y0=- (x-x0),
由于y0≠0,
可得x=- y+2+x0,
代入抛物线方程得y2+ y-8-4x0=0.
所以y0+y1=- ,
可求得y1=-y0- ,x1= +x0+4,
所以点B到直线AE的距离为
d=
=
=4 .
则△ABE的面积S= ×4 ≥16,
当且仅当 =x0,即x0=1时等号成立.
所以△ABE的面积的最小值为16.
25. (201 4山西忻州一中、康杰中学、临汾一中、长治二中四校高三第三次联考,20) 抛物线C1: 的焦点与椭圆C2: 的一个焦点相同. 设椭圆的右顶点为A,C1, C2在第一象限的交点为B,O为坐标原点,且 的面积为 .
(1) 求椭圆C2的标准方程;
(2)过A点作直线 交C1于C, D两点,连接OC, OD分别交C2于E, F两点,记 , 的面积分别为 , . 问是否存在上述直线 使得 ,若存在,求直线 的方程;若不存在,请说明理由.
[答案] 25.查看解析
[解析] 25. (1)∵ ∴焦点 ∴ 即 ……………1分
又∵ ∴ ……………2分
代入抛物线方程得 . 又B点在椭圆上得 ,
∴椭圆C2的标准方程为 . ……………4分
(2)设直线 的方程为 ,由 得
设 ,所以 ……………6分
又因为
直线 的斜率为 ,故直线 的方程为 ,
由 得 ,同理
所以
则 , ……………10分
所以 ,
所以 ,故不存在直线 使得 ……………12分
26. (2014福州高中毕业班质量检测, 19) 已知动圆 过定点 , 且与直线 相切.
(Ⅰ)求动圆圆心 的轨迹方程;
(Ⅱ)设 、 是轨迹 上异于原点 的两个不同点, 直线 和 的倾斜角分别为 和 ,
①当 = 时, 求证直线 恒过一定点 ;
②若 为定值 , 直线 是否仍恒过一定点, 若存在, 试求出定点的坐标;若不存在, 请说明理由.
[答案] 26.查看解析
[解析] 26.(Ⅰ) 设动圆圆心 , 依题意点 的轨迹是以 为焦点,直线 为准线的抛物线,其方程为 . (3分)
(Ⅱ) 设 , . 由题意得 (否则 ) 且 ,
则 ,所以直线 的斜率存在, 设直线 的方程为 ,
则将 与 联立消去 , 得 ,
由韦达定理得 -------※(6分)
①当 = 时, 所以 ,
所以 , 又由※知: ,所以 ;因此直线 的方程可表示为 , 所以直线 恒过定点(-4,0).
②当 为定值 时. 若 = , 由①知,
直线 恒过定点 ,(9分)
当 时, 由 , 得 = =
将※式代入上式整理化简可得: , 所以 ,
此时,直线 的方程可表示为y=kx+ ,
所以直线 恒过定点 ,
所以当 时, 直线 恒过定点(-4,0).,
当 时直线 恒过定点 . (13分)
27. (2014河北石家庄高中毕业班复习教学质量检测(二),20) 已知动圆 过定点 ,且在 轴上截得弦长为4. 设该动圆圆心的轨迹为曲线 .
(Ⅰ)求曲线 方程;
(Ⅱ)点 为直线 : 上任意一点,过 作曲线 的切线,切点分别为 、 , 面积的最小值及此时点 的坐标.
[答案] 27.查看解析
[解析] 27.(Ⅰ)设动圆圆心坐标为 ,根据题意得:
,化简得 . (4分)
(Ⅱ)解法一:设直线 的方程为 ,
由 消去 得 ,
设 ,则 ,且 ,(6分)
以点 为切点的切线的斜率为 ,
其切线方程为 ,即 ,
同理过点 的切线的方程为 ,
设两条切线的交点为 在直线 上,
,解得 ,即 ,
则 ,即 ,(8分)
代入 ,
,
到直线 的距离为 ,
,
,
当 时, 最小,其最小值为 ,此时点 的坐标为 . (12分)
解法二:设 在直线 上,点 在抛物线 上,
则以点 为切点的切线的斜率为 ,
其切线方程为 ,即 ,
同理以点 为切点的方程为 ,(6分)
设两条切线的均过点 ,则 ,
点 、 的坐标均满足方程 ,
即直线 的方程为: ,(8分)
代入抛物线方程 消去 可得: ,
直线 的距离为 ,
,
当 时, 最小,其最小值为 ,此时点 的坐标为 . (12分)
28.(2014湖北八校高三第二次联考数学(理)试题,21)如图所示,已知椭圆C1和抛物线C2有公共焦点 , C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线 与抛物线C2分别相交于A、B两点.
(Ⅰ)写出抛物线C2的标准方程;
(Ⅱ)求证:以AB为直径的圆过原点;
(Ⅲ)若坐标原点 关于直线 的对称点 在抛物线C2上,直线 与椭圆C1有公共点,求椭圆C1的长轴长的最小值.
[答案] 28.查看解析
[解析] 28. (1) 设抛物线的标准方程为
由 得 ,
; …………………3分
(2) 可设 , 联立 得 ,
设
, 即以 为直径的圆过原点; ………………8分
(3) 设 , 则
得
………………10分
设椭圆 ,与直线 联立可得:
∴长轴长最小值为 ………………13分
29. (2014吉林高中毕业班上学期期末复习检测, 21) 已知抛物线 : 的准线为 ,焦点为 , 的圆心在 轴的正半轴上,且与 轴相切,过原点作倾斜角为 的直线 ,交 于点 ,交 于另一点 ,且
(Ⅰ) 求 和抛物线 的方程;
(Ⅱ) 过 上的动点 作 的切线,切点为 、 ,求当坐标原点 到直线 的距离取得最大值时,四边形 的面积.
[答案] 29.查看解析
[解析] 29. (Ⅰ)准线 交 轴于 ,在 中 ,
所以 , 所以 ,抛物线方程是 , (3分)
在 中有 , 所以 ,
所以⊙ 方程是: . (6分)
(Ⅱ)解法一:设 ,
所以切线 ;切线 , (8分)
因为 和 交于 点,所以 和 成立 ,
所以ST方程: , (10分)
所以原点到 距离 ,当 ,即 在y轴上时 有最大值,
此时直线ST方程是 ,
所以 ,
所以此时四边形 的面积 . (12分)
圆锥曲线高考题(三)
程序框图作业专练
姓名:__________班级:__________考号:__________
题号 一 二 总分
得分
一 、选择题(本大题共15小题,每小题5分,共75分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
1.(2015四川高考真题)执行如图所示的程序框图,输出S的值为( )
(A)- (B) (C)- (D)
2.(2015新课标2高考真题)右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的 分别为14,18,则输出的 为( )
3.执行如图所示的程序框图,输出S的值为( )
A. 0 B. ﹣1 C. ﹣ D. ﹣
4.执行如图所示的程序框图,如果输入的 的值是6,那么输出的 的值是( )
A.15 B.105 C.120 D.720
5.当 时,执行如右图所示的程序框图,
输出的 值为
A. 30 B.14 C. 8 D. 6
6.(2015•上海模拟)某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
A. f(x)=x2 B. C. D.
7.阅读右侧程序框图,如果输出 ,那么在空白
矩形框中应填入的语句为
A. B. C. D.
8.右图中, 为某次考试三个评阅人对同一道题的独立评分, 为该题的最终得分,当 时, 等于
A. B. C. D.
9.执行如右图所示的程序框图,若输入的 值等于7,则输出的 的值为
A.15 B.16 C.21 D.22
10.如图是一个算法的程序框图,该算法所输出的结果是( )
A. 34 B. 23 C. 12 D. 45
11.执行如图所示的程序框图,当输出值为4时,输入 的值为
A.2 B. C.-2或-3 D.2或-3
12.如图1是某县参加 年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160~185cm(含160cm,不含185cm)的学生人数,那么在流程图中的判断框内应填写的条件是( )
A.i<9 B.i<8 C.i<7 D.i<6
13.如果执行下图所示的框图,输入 ,则输出的数等于( )
A. B. C. D.
14.根据右边框图,对大于2的整数 ,得出数列的通项公式是( )
15.如图所示,程序框图(算法流程图)的输出结果是( )
(A)34 (B)55 (C)78 (D)89
二 、填空题(本大题共5小题,每小题5分,共25分)
16.执行如图所示的程序框图,则输出的结果是 ;
17.(2015•泰州一模)执行如图所示的流程图,则输出的n为 .
18. 如右图所示的程序框图的输出值 , 则输入值 。
19.阅读右边的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为 .
20.阅读右边的框图,运行相应的程序,输出 的值为________.
0.衡水万卷作业卷三十二文数答案解析
一 、选择题
1.【答案】D
【解析】第四次循环后,k=5,输出S=sin = ,选D
2.B
【解析】
试题分析:由题意输出的a是18,14的最大公约数2,故选B.
考点:1. 更相减损术;2.程序框图.
3.【考点】: 程序框图.
【专题】: 图表型;算法和程序框图.
【分析】: 模拟执行程序框图,依次写出每次循环得到的S,n的值,当n=7时n大于5退出循环,输出S的值为0.
【解析】: 解:模拟执行程序框图,可得
S=0,n=1
S= ,n=3,n不大于5
S=﹣ ,n=5,n不大于5
S=0,n=7,n大于5
退出循环,输出S的值为0,
故选:A.
【点评】: 本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的S,n的值是解题的关键,属于基础题.
4.B
5.B
6.【考点】: 选择结构.
【专题】: 压轴题;图表型.
【分析】: 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)+f(﹣x)=0,即函数f(x)为奇函数②f(x)存在零点,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
【解析】: 解:∵A:f(x)=x2、C:f(x)=x2,D:f(x)= 不是奇函数,故不满足条件①
又∵B: 的函数图象与x轴没有交点,故不满足条件②
而C: 既是奇函数,而且函数图象与x也有交点,
故C:f(x)=sinx符合输出的条件
故答案为C.
【点评】: 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.
7.A
8.C
9.B
10.【答案】A
解析:第一次执行循环体得i=2,m=1,n= ,第二次执行循环体得i=3,m=2,n= ,第三次执行循环体得i=4,m=3,n= ,此时i≥4,则跳出循环体,所以输出的n的值为34,则选A.
【思路点拨】遇到循环结构程序框图时,可依次执行循环体,直到跳出循环,再进行判断.
11.D
12.A解:现要统计的是身高在cm之间的学生的人数,由图1可知应该从第四组数据累加到第八组数据,即是要计算 的和,故流程图中空白框应是 当 时就会返回进行叠加运算,当 将数据直接输出,不再进行任何的返回叠加运算,故 .故选A。
13.【知识点】算法与程序框图.
【答案】A
解析:程序运行的结果为
= ,故选A.
【思路点拨】根据程序框图中的循环规律知,S是数列 的前5项和,利用裂项求和法求出其值即可.
14.C
15.B
二 、填空题
16.132
17.【考点】: 程序框图.
【专题】: 图表型;算法和程序框图.
【分析】: 模拟执行程序框图,依次写出每次循环得到的S,n的值,当S=63时,不满足条件S>63,退出循环,输出n的值为4.
【解析】: 解:模拟执行程序框图,可得
S=511,n=1
满足条件S>63,S=255,n=2
满足条件S>63,S=127,n=3
满足条件S>63,S=63,n=4
不满足条件S>63,退出循环,输出n的值为4.
故答案为:4.
【点评】: 本题主要考查了程序框图和算法,正确得到每次循环的S,n的值是解题的关键,属于基础题.
18.
19.3
20.-4
解: 时, ; 时, ,所以输出的 的值为-4.
圆锥曲线高考题相关热词搜索:圆锥曲线
最新推荐成考报名
更多- 歇后语_歇后语大全_歇后语大全及答案_爆笑歇后语
- 大学排名_大学排名2018排行_大学查询_中国大学名单
- 成语大全_四字成语_在线成语词典_成语查询
- 成语接龙大全查询,成语接龙游戏,在线成语接龙
- 全国安全教育平台入口_学校安全教育平台
- 社保查询网-社会保障卡查询,社会保险查询,社保网上查询
- 汉字简体繁体转换_在线繁体字转换工具
- 数字大写转换|人民币金额(数字)大小写转换在线工具
- 年龄计算器实际岁数计算器 - 周岁虚岁计算器
- 产假计算器-算产假计算器在线2018-2018年产假自动计算器
- 预产期计算器-怀孕孕期计算器-怀孕天数计算
- 中国文库网-教育资源网-范文文章
- 邮编区号查询网
- 致富商机网-致富点子_创业项目
- 创业项目网--最热门的投资项目
- 中国邮政邮编查询号码
- 电话区号查询
- 全国车牌号归属地大全
- 在线网速测试|宽带速度测试
- 人民币汇率查询
- ●理财有没有风险 金融互联网理财
- ●qq网名
- ●2016最新伤感说说
- ●谈笑风生造句
- ●读书的名言
- ●资产清查报告
- ●贫困户申请书
- ●财务自查报告
- ●离婚起诉书
- ●赞美老师的演讲稿
- ●车间管理
- ●车辆购置税
- ●跨越百年的美丽读后感
- ●跟女友离别的话
- ●超市管理制度
- ●起诉状范本
- ●赠别诗大全
- ●描写夏天的句子
- ●描写友谊的诗句
- ●迁户口申请书
- ●转正申请表范本
- ●这个杀手不太冷台词
- ●运动会稿子精选
- ●那么那么造句
- ●送给男朋友的情话大全
- ●钳工实训报告
- ●霸气说说大全
- ●骂人不带脏字的
- ●幼儿园见习个人总结
- ●追女孩子的短信

